ML | 算法流程与最佳属性选择

发表于 2019-03-15 分类于 ML Waline：阅读次数：本文字数： 2.9k 阅读时长 ≈ 11 分钟

决策树基本流程

总体流程

“分而治之”（divide-and-conquer）

自根至叶的递归过程
在每个中间结点寻找一个“划分”（split or test）属性

三种停止条件

当前结点包含的样本全属于同一类别，无需划分
当前属性集为空，或是所有样本在所有属性上取值相同（类别不同），无法划分
当前结点包含的样本集合为空，不能划分

基本流程

决策树基本流程

图来自周志华《机器学习》P.74

属性集 $A$ ：就是类似前面提到的年龄、长相、工作等属性特征

划分选择

由上图可以看出，决策树学习的关键是第 8 行，即如何选择最优划分属性。一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”（purity）越来越高

ID3

ID3(Iterative Dichotomiser)是以信息增益为准则来选择划分属性的决策树学习算法，迭代二分器的简称

信息熵（information entropy）

“信息熵”是度量样本集合“纯度”最常用的一种指标，假定当前样本集合 $D$ 中的第 $k$ 类样本所占比例 $p_k(k=1,2,...,|y|)$ ，则信息熵定义为：

Ent(D)=-\sum_{k=1}^{|y|}p_klog_2p_k \tag{1}

$Ent(D)$ 的值越小，则 $D$ 的纯度越高。

类似《信息论》中的信源熵 $H(x)$ ，即信源输入一个消息所提供的平均信息量或者信源的不肯定程度

例如：一个选择题，有 ABCD 四个选项，如果对 ABCD 四个选项的肯定程度是差不多的，即每个的概率为 $\frac{1}{4}$ ，此时不确定性最高，纯度相对而言是最低的。

两种特殊情况：

（等概情况）如果 $p_k$ 有 m 类，每个 $p_k$ 都为 $\frac{1}{m}$ 的话，信息熵取得一个最大值 $log_2{|y|}$ ，我们是最不确定的，即纯度最低。
（确定情况）如果 $p=0或1$ ，则信息熵为 0，纯度最高

树的构建过程，是让我们的不确定性往下降（即提升纯度），最简单的选择方法是使用信息增益。信息增益直接以信息熵为基础，计算当前划分对信息熵所造成的变化。

信息增益（information gain）

假定离散属性 $a$ 有 $V$ 个可能取值 $\lbrace a^1,a^2,a^3,...,a^V \rbrace$ ，若使用 $a$ 来对样本集 $D$ 进行划分，则会产生 $V$ 个分支结点，其中第 $v$ 个分支结点包含了 $D$ 中所有在属性 $a$ 上取值为 $a^v$ 的样本，记为 $D^V$ 。

以一个女孩去选相亲对象的例子，用人话来说

所谓离散属性 $a$ 就是这个特征（或属性）有可以穷尽的离散取值，如下面的属性集合 $A=\lbrace a^1（长相）,a^2 （年龄）,a^3（收入） \rbrace$ ，长相你可以定义为帅或者不帅（只有 2 个有限取值）

$D^V$ 是以某属性对 $D$ 进行划分的子集，如“长相”则可得到 2 个子集，记为 $D^1(长相=帅)$ ， $D^2(长相=不帅)$

$D^1$ 里则有 1 号 xxx，2 号 xxx 等备选对象

我们计算出 $D^V$ 的信息熵，再考虑到不同分支结点所包含的样本数不同，给分支结点赋予权重 $\frac{|D^v|}{|D|}$ （即样本数越多的分支结点影响越大)，于是可以属性 $a$ 对样本集 $D$ 进行划分所获得的“信息增益”：

Gain(D,a)=Ent(D)-\sum_{v=1}^V \frac{|D^v|}{|D|}Ent(D^v) \tag{2}

一般而言，信息增益越大，意味着使用属性 $a$ 来进行划分所获得的“纯度提升”越大。因此，我们可以用信息增益来进行决策树的划分属性选择。

信息增益示例：

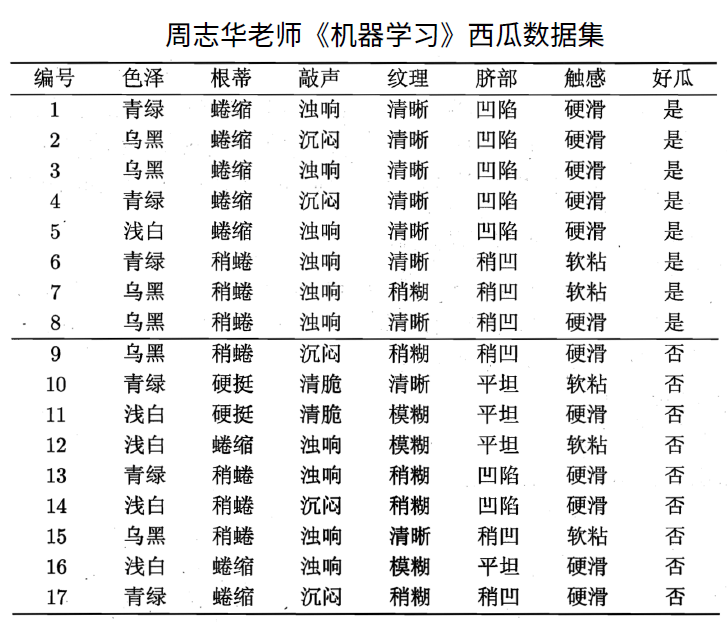
以周志华老师的西瓜为例：

西瓜数据集

好瓜为标签列（label），其他为属性（特征）列

该数据集包含 17 个训练样例，结果有 2 个类别 $|y|=2$ ，在决策树学习开始时，根结点包含 $D$ 中的所有样例，其中正例占 $p_1=\frac{8}{17}$ ，反例占 $p_2=\frac{9}{17}$ ，则可以计算出根节点的信息熵为：

Ent(D) =-\sum_{k=1}^2p_k log_2 p_k =-(\frac{8}{17}log_2\frac{8}{17}+\frac{9}{17}log_2\frac{9}{17}) =0.998

对属性做如下定义：

a^1(色泽)，a^2(根蒂)，a^3(敲声)，a^4(纹理)，a^5(脐部)，a^6(触感)

以属性“ $a^1(色泽)$ ”为例，其对应的 3 个数据子集分别为 $D^1(色泽=青绿),D^2(色泽=乌黑),D^3(色泽=浅白)$ 。

子集 $D^1$ 包含编号为 $\lbrace 1,4,6,10,13,17\rbrace$ 的 6 个样例，其中正例占 $p_1=\frac{3}{6}$ ，反例占 $p_2=\frac{3}{6}$ ， $D^2$ 、 $D^3$ 同理，3 个结点的信息熵为

\begin{aligned}Ent(D^1)=-(\frac {3}{6}log_2\frac{3}{6}+\frac {3}{6}log_2\frac{3}{6})=1.000\\Ent(D^2)=-(\frac {4}{6}log_2\frac{4}{6}+\frac {2}{6}log_2\frac{2}{6})=0.918\\Ent(D^3)=-(\frac {1}{5}log_2\frac{1}{5}+\frac {4}{5}log_2\frac{4}{5})=0.722 \end{aligned}

所以，属性“色泽”的信息增益为

\begin{aligned}Gain(D,色泽)&=Ent(D)-\sum_{v=1}^3\frac{|D^v|}{|D|}Ent(D^v) \\&=0.998-(\frac{6}{17}\times1.000+\frac{6}{17}\times0.918+\frac{5}{17}\times0.722)\\&=0.109 \end{aligned}

同样的方法，计算其他属性的信息增益为

\begin{aligned} &Gain(D,根蒂)=0.143 \qquad Gain(D,敲声)=0.141\\ &Gain(D,纹理)=0.381 \qquad Gain(D,脐部)=0.289\\ &Gain(D,触感)=0.006 \end{aligned}

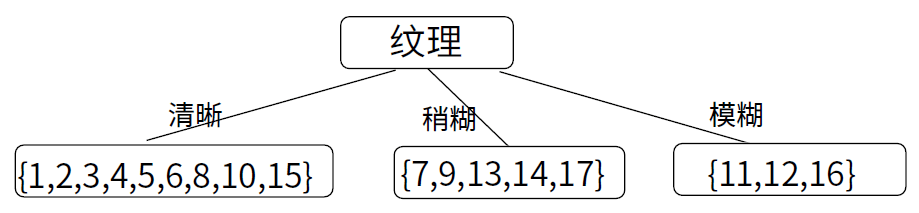
显然，属性“纹理”的信息增益最大，其被选为从根结点往下做第一次划分的属性

所以清晰、稍糊、模糊作为三个不同的数据子集，完成第一次数据的划分。然后，决策树学习算法将对每个分支结点做进一步划分。以第一个分支结点（“纹理=清晰”）为例，该结点包含的样例集合 $D^1$ 中有编号为 $\lbrace 1,2,3,4,5,6,8,10,15\rbrace$ 的 9 个样例，可用属性集合为 $\lbrace 色泽,根蒂,敲声,脐部,触感\rbrace$ 。基于 $D^1$ 计算出各属性的增益：

\begin{aligned} &Gain(D^1,色泽)=0.043 \qquad Gain(D^1,根蒂)=0.458\\ &Gain(D^1,敲声)=0.331 \qquad Gain(D^1,脐部)=0.458\\ &Gain(D^1,触感)=0.458 \end{aligned}

此时“纹理”不再作为候选划分属性

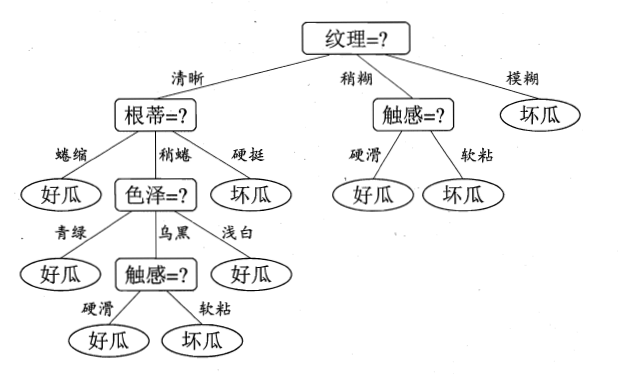
“根蒂”、“脐部”、“触感”3 个属性均取得了最大的信息增益，可任选其中之一作为划分属性。这里我们选择“根蒂”作为划分属性，然后递归的去完成这样的过程，对每个分支结点进行上述操作。最终得到的决策树如下图所示。

信息增益决策树

小结：划分时选择增益最大的

C4.5

可能你已经发现了，在上面的介绍中，我们有意忽略了“编号”这一列。若把“编号”也作为一个候选划分属性，则根据公式(2)计算出它的信息增益达到了 0.998，远远大于其他划分属性。若每个编号产生一个分支，我们可以用决策树桩（即一层分类）把所有的瓜都区分出来。但是，“编号”作为一个属性划分是不具备泛化能力的，因为你拿到的测试集上并没有对应号值的西瓜。

将“编号”带入信息增益公式，也可以得出一样的结论

实际上，信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，著名的 C4.5 决策树算法不直接使用信息增益，而是使用“增益率”（gain ratio）来选择最优划分属性。

增益率

增益率定义为

Gain\_ratio(D,a)=\frac{Gain(D,a)}{Ⅳ(a)}

其中

Ⅳ(a)=-\sum_{v=1}^V \frac{|D^v|}{D}log_2\frac{|D^v|}{D}

称为属性 $a$ 的“固有值”（intrinsic value）。属性 $a$ 的可能取值数目越多（即 $V$ 越大），则 $Ⅳ(a)$ 的值通常会越大。例如

\begin{aligned} & Ⅳ(触感)=0.874(V=2)\quad Ⅳ(色泽)=1.580(V=3) \quad Ⅳ(根蒂)=1.402(V=3)\\ & Ⅳ(敲声)=0.973(V=3) \quad Ⅳ(纹理)=1.447(V=3) \quad Ⅳ(脐部)=1.549(V=3)\\ & Ⅳ(编号)=4.088(V=17) \end{aligned}

这样会有一个相对公正的权衡。需要注意的是，增益率准则对可取值数目（ $V$ ）少的属性有所偏好，因此，C4.5算法不是直接选择增益率最大的候选划分属性，而是使用了一个启发式[Quinlan, 1993]：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

所谓启发式，就是先求出固有值 $Ⅳ(a)$ 的平均值（本例： $Ⅳ(avg)=1.704$ ），然后将明显高于平均值的值（本例： $Ⅳ(编号)=4.088(V=17)$ ）直接剔除后（即排除异常样本），再选增益率最高的（本例：$ Ⅳ(色泽)=1.580(V=3)$ ）作为划分属性

CART

CART(Classification and Regression Tree) 是一种著名的二分类决策树学习算法，分类和回归任务都可用。CARRT 决策树使用“基尼指数”（Gini index）来选择划分属性。

此处不再是根据信息熵、信息增益、信息增益率来定义了，而是选择了纯度（类别相近的概率有多高）

基尼指数

是一种不等性度量；
通常用来度量收入不平衡，可以用来度量任何不均匀分布；
是介于 0~1 之间的数，0 完全相等，1 完全不相等；
总体内包含的类别越杂乱，GINI 指数就越大（跟熵的概念很相似）

数据集 $D$ 的纯度可用基尼值来度量

\begin{aligned} Gini(D)&=\sum_{k=1}^{|y|}\sum_{k'\not= k}p_kp_{k'} \qquad p_k'=1-p_k\\ &=1-\sum_{k=1}^{|y|}p_k^2 \end{aligned}

直观来说， $Gini(D)$ 反映了从数据集 $D$ 中随机抽取两个样本，其类别标记不一致的概率。因此 $Gini(D)$ 越小，数据集 $D$ 的纯度越高。

属性 $a$ 的基尼指数定义为

Gini\_index(D,a)=\sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)

于是，我们在候选属性集合 $A$ 中，选择那个使得划分后基尼指数最小的属性作为最优划分属性，即 $a_*=arg\,min\,Gini\_index(D,a) \quad a\in A$ 。

举例来说，就是一堆人有男有女，你随机找两个出来看看性别是否不同，这个概率越大就证明越不纯

以“纹理”属性为例，其对应的 3 个数据子集分别为 $D^1(纹理=清晰),D^2(纹理=稍糊),D^3(纹理=模糊)$ 。

子集 $D^1$ 包含编号为 $\{ 1,2,3,4,5,6,8,10\}$ 的 9 个样例，其中正例占 $p_1=\frac{7}{9}$ ，反例占 $p_2=\frac{2}{9}$ ， $D^2$ 、 $D^3$ 同理，则属性“纹理”的基尼指数为：

\begin{aligned} Gini\_index(D,纹理) &= \frac{9}{17}×Gini(D_1)+\frac{5}{17}×Gini(D_2)+\frac{3}{17}×Gini(D_3) \\ & = \frac{9}{17}×\{1-[(\frac{7}{9})^2+(\frac{2}{9})^2]\}+\frac{5}{17}×\{1-[(\frac{1}{5})^2+(\frac{4}{5})^2]\}+\frac{3}{17}×[1-(0^2+1^2)] \\ & = 0.27712 \end{aligned}

同理可以算出其他属性的基尼指数，比如 $Gini\_index(D,色泽)= 0.515$ 。这里“纹理”的基尼指数比“色泽”小，若是在这两者中选择结点的话，就会选择“纹理”作为划分属性。（其他特征的基尼指数没有算，懒，所以这个结点不一定是“纹理”）

参考资料

CART 算法中的基尼指数
周志华-《机器学习》

若有错误或其它问题欢迎留言评论交流指出哦。