ML | 机器学习中的评估指标

发表于 2019-02-28 分类于 ML Waline：阅读次数：本文字数： 990 阅读时长 ≈ 4 分钟

机器学习的目标

给定的训练数据上，学习出来一个能够归纳这些数据分布特征的模型，能在新的未知的样本上预测有好的效果

问题 ①： 什么模型好？

泛化能力强的模型，即能很好的适用于没见过的样本，判断指标有如：错误率低、精度高

机器学习的评估方法

关键：获得可靠的“测试集数据”（test set）？

测试集（用于评估）应该与训练集（用于模型学习）“互斥”

常见方法：

留出法（hold-out）
交叉验证法（cross validation）
自助法（booststrap）

① 留出法

即一份资料总共有 100 道题，拿 90 道来学习（训练集），剩下 10 道来检验（测试集）

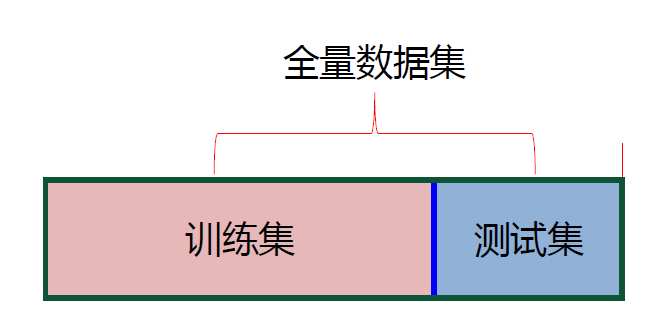
图1 留出法

注意点：

保持数据分布一致性（例如：分层采样）
多次重复划分（例如：100 次随机划分）
测试集不能太大、不能太小（例如：1/5~1/3）

② k 折交叉验证

一图胜过千言万语

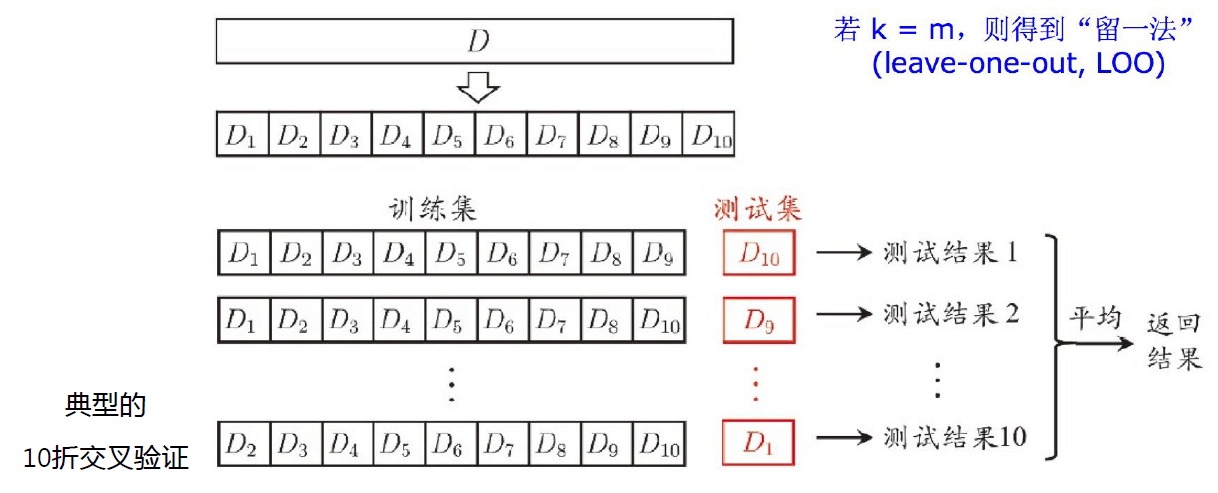
图2 k折交叉验证

m 指样本个数

特点：

优点：更公平可靠
缺点：运算量大

③ 自助法

基于“自助采样”的方法（bootstrap sampling），又称：“有放回采样”、“可重复采样”

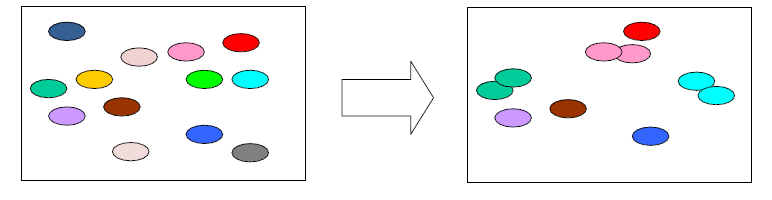
图3 自助法

注意，当数据量非常大时，约有 36.8%的样本不会被抽取，如下

$\lim\limits_{x\to+\infty}(1-\frac{1}{m})^m \Rightarrow \frac{1}{e}\approx0.368$

特点：

训练集与原样本集同规模
数据分布有所改变（因为可能多次抽到同一个样本）

测试集

“包外估计”（out-of-bag estimation）：即那为被抽取的样本作为测试集

机器学习的评估度量标准

性能度量（performancemeasure）

是衡量模型泛化能力的数值评价标准，反映了当前问题（任务需求）
使用同的性能度量可能会导致不同的评判结果

关于模型“好坏”的判断，不仅取决于算法和数据，还取决于当前任务需求。

比如：回归（regression）任务常用均方差： $E(f;D)=\frac{1}{m}\sum\limits_{i=1}^{m}(f({x}_i)-y_i)^2$

错误率：

E(f;D)=\frac{1}{m}\sum\limits_{i=1}^{m}\mathbb{I}(f({x}_i)\neq y_i)

$E(f;D)$ 表示数据集 D 上用 f 作为假设（模型）的错误率

$\mathbb{I}$ 是指示函数，当括号里条件为真的时候取 1，条件为假的时候取 0

$\mathbb{I}$ 不等同于后面的 sign 函数，符号函数是大于 0 返回 1，小于 0 返回-1

精度：

\begin{aligned} E(f;D)&=\frac{1}{m}\sum\limits_{i=1}^{m}\mathbb{I}(f(\boldsymbol{x}_i) = y_i)\\&=1- E(f;D)\end{aligned}

二分类混淆矩阵 Confusion Matrix

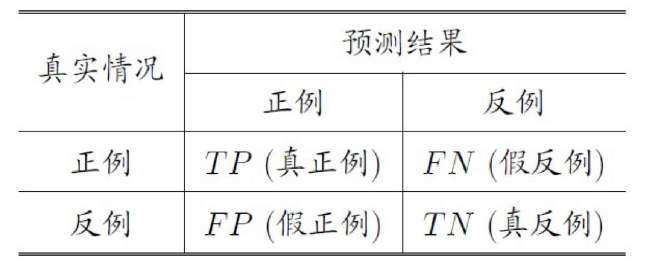
图4 混淆矩阵

True positive (TP)

真实值为 Positive，预测正确（预测值为 Positive）

True negative (TN)

真实值为 Negative，预测正确（预测值为 Negative）

False positive (FP)

真实值为 Negative，预测错误（预测值为 Positive），第一类错误， Type I error

False negative (FN)

真实值为 Positive，预测错误（预测值为 Negative），第二类错误， Type II error

准确率（查准率） Precision

Precision 是分类器预测的正样本中预测正确的比例，取值范围为[0,1]，取值越大，模型预测能力越好。

P=\frac{TP}{TP+FP}

召回率（查全率）Recall

Recall 是分类器所识别出的正样本占所有正样本的比例，取值范围为[0,1]，取值越大，模型预测能力越好。

R=\frac{TP}{TP+FN}

$F_\beta sore$

Precision 和 Recall 是互相影响的，理想情况下肯定是做到两者都高，但是一般情况下 Precision 高、Recall 就低，Recall 高、Precision 就低。为了均衡两个指标，我们可以采用 Precision 和 Recall 的加权调和平均（weighted harmonic mean）来衡量，即，公式如下：

F_\beta sore=(1+\beta^2)\times\frac{P\times R}{\beta^2\times P+R}

$\beta$ 为权重

F_\beta =F_1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{样例总数+TP-TN}